數學菜鳥的AI學習攻略

　　

　　大數據文摘作品，轉載要求見文末

　　原作者 | Daniel Jeffries

　　編譯 | Molly 寒小陽

　　「

　　自學AI的過程中，我們非常需要理解這些數學符號。它可以讓你用一種非常簡潔的方式來表達一個複雜的想法。

　　」

　　你是否跟我一樣，自幼恨透數學。

　　現在，我終於發現了我對數學絕緣的最主要原因：我的老師從來不去回答最重要的問題：我為什麼要學數學？學數學有什麼用？

　　他們只是在黑板上寫下一大堆方程，並讓我記下來。

　　現在，如果你對AI這個激動人心的領域感興趣，那麼它將是回答這個問題最好的答案！那就是，我想要寫一個更好的圖像識別程序，或者一個可以理解自然語言的交互界面！也許甚至想有一天寫出自己的演演算法？

　　如果你想從閱讀 arXiv（https://arxiv.org/list/cs.AI/recent） 上的幾篇論文開啟自學AI之路？那麼首先，你需要知道怎樣理解這些有意思的數學小符號。

　　也許，學習數學符號最重要的原因，就是它可以讓你用一種非常簡潔的方式來表達一個複雜的想法。

　　沒有它，解釋每個方程，都需要花上很多頁的篇幅。

　　而這篇文章要告訴你的是，學習這些符號不像你想象的那麼難。

　　讓很多人對數學失去信息的第二個原因是，很多解釋寫得太可怕了。

　　事實上，大部分人並不擅長解釋東西。人們一般要定義一個數學術語，會使用更多的數學術語。這就造成了不理解的一個無限循環。好比定義「大象」這個詞，說，「大象就是大象一類的東西。」

　　這篇文章會將數學符號和現實世界關聯起來，並使用你已知的東西來類比。這樣你可以腳踏實地地學習。

　　

　　但是，這篇文章無法覆蓋到你讀一篇論文需要的所有數學符號。所以你會需要一本超級凝練的數學符號指南，Edward R. Scheinerman的Mathematical Notation: A Guide for Engineers and Scientists 。（它是我數學菜鳥的AI學習攻略 文章的一個後繼補充，但它是我使用最頻繁的一本書。它現在滿是高亮和折頁。隨著數學知識的不斷擴充，我一遍又一遍地回頭翻閱這本書。）

　　讓我們開始吧。

　　首先，什麼是演演算法？

　　它真的只是解決一個特定的問題的一系列步驟。無論你是否意識到，你都在使用演演算法。如果你需要給孩子們打包午飯，送他們上學，取走乾洗的衣服，然後去上班，你已經無意識地構造了一系列步驟，從廚房到辦公室。這就是一個演演算法。

　　如果你的老闆同時給你安排了六項工作，你需要找到在一天內完成它們的最好的方式。你需要選擇哪些事先做，哪些事後做，哪些事一起做等等。這就是一個演演算法。

　　這個概念為什麼很重要呢？因為一個方程也不過是解決問題的一系列步驟而已。

　　我們從一些簡單的符號開始，寫一些方程。數學就是對事物的翻譯。我們有一個輸入和一個輸出。我們將一些東西代入到我們方程的變數中，遍歷所有的步驟，然後得到輸出。計算機也是同樣的道理。

　　目前，神經網路背後的大部分黑魔法來自於數學的三個分支：

　　線性代數

　　集論

　　微積分

　　集合是什麼？它就是一堆東西。一般使用花括弧{ }或方括弧括起來。（搞數學的傢伙對所有東西都很難在最佳符號表達上達成一致。）

　　

　　一個集合

　　還記得我們在第4部分看到的張量？那就是一個集合。

　　

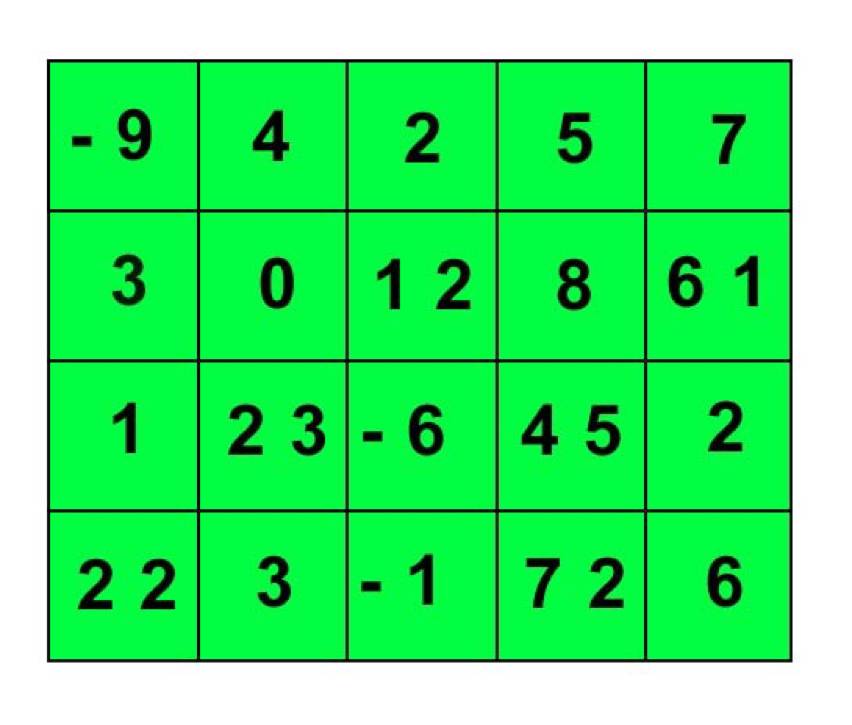
　　一個集合通常由大寫字母表示，例如A、B、V或W。只要你前後一致，字母本身是什麼並不重要。

　　但是，一些特定的大寫字母和符號被保留下來，用來表示重要的、常用的數字集，例如：

　　∅ = 空集（集合里什麼都沒有）。這個符號是一個希臘字母，「phi」。數學里常常會用到希臘字母。此處可以查閱大小寫希臘字母的寫法（https://en.wikipedia.org/wiki/Greek_letters_used_in_mathematics,_science,_and_engineering）。

　　R =所有實數。（幾乎所有存在的數都是實數，包括整數、分數、超越數如Pi (π)(3.14159265…)。但是不包括虛數，一種為了求無解方程的解而構造的數，也不包括無窮）

　　Z =所有整數。（除了分數之外的數字，比如-1,-2, 0, 1, 2, 3）

　　大部分保留字母表可以在趣味數學（http://www.mathsisfun.com/sets/number-types.html）里查到。

　　所有這些都是集合，其中一部分是子集，也就是他們被更大的一個集合完全包含，就像這樣：

　　

　　去查查看Q和N是什麼意思吧！

　　在這個例子中，我們可以說，Z（整數集）是R（實數集）的子集。

　　我們可以這麼寫：

　　A是B的子集（A包含於B）：相反的，B是A的超集（B包含A）

　　

　　；

　　

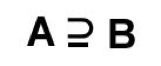
　　我為什麼要在乎一個集合B是不是包含了A的全部內容呢？好問題。

　　假如有一個集合，包括了所有生活在美國的人，有他們的年齡、地址等等信息。現在假設有另一個集合，包括了心臟病發病率更高的人。那麼這兩個集合重合的地方，可以告訴我們哪個地區的人更可能患有心臟病。

　　每個集合里都有元素。元素是什麼？就是大集合的一部分。我們再看一下我們的張量。

　　

　　我們將集合中的元素記作小寫斜體字母，例如x.我們用一個看起來很奇怪的E一樣的符號（其實不是E），來表示一個元素是集合的一部分。我們可以這麼寫：

　　

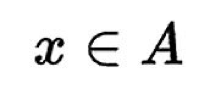
　　這表示x是集合A中的一個元素。

　　我們也可以說x不是集合A中的一個元素：

　　

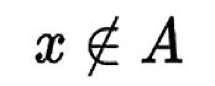
　　你越能理解這些符號，你就越能在頭腦中通過這些字元串來溝通。當你看到上面這個，你可以說，「x不是集合A中的元素。」你越能明確地講出符號的含義，你就越能理解它們。

　　當然，寫出一個集合的所有元素是不現實的，我們可以使用一種特殊的方式來寫出一個元素的序列。假如我們有一個數字序列，以1為步長遞增。我們可以這樣寫：

　　x = {1,2,3,4…n}

　　這些點表示這個序列到n結束，n代表「序列的末尾」。所以如果n = 10,這個集合包括從1到10的數字範圍。如果n = 100,這個集合包括從1到100的數字範圍。

　　瘋狂的方程

　　當我們將集合轉化為線性代數的時候，它們就十分有意思了。你已經認識了一些代數符號比如加號+，減號-。現在我們看兩個新的符號和一個方程。首先是符號：

　　Σ = 一系列數字的和

　　Π = 一系列數字的積

　　和是什麼？是序列中所有數字做加法。比如我們有一個向量集A（記住向量是一行或一列數字）包括： {1,2,3,4,5}.

　　序列的和為：

　　1 + 2 + 3 + 4 + 5 = 15

　　積是所有數字做乘法。所以對於同樣的集合A我們有：

　　1 x 2 x 3 x 4 x 5 =120

　　我們可以將序列的和精簡地寫作：

　　

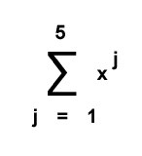
　　那麼我們怎樣理解它呢？簡單，看這個。

　　

　　我們從底部的j開始，j是一個變數。然後將j代入到右邊的表達式中。最後，我們將序列的結束數字寫在頂部。看一個例子：

　　

　　如果你是一個程序員，你會立刻認出這是一個循環！

　　我們給這個方程寫一個Python函數：

　　def sum_x_range(x):    j = 1    output = []   # 創建一個空list    for k in range(0,5):  # 開始循環         z = x**j      # 計算x的j次方         j = j + 1     # j增加1，知道到達n，也就是5

　　output.append[z]   # 將z添加到list中    return sum(output)  # 返回list中所有數字的和

　　print (sum_x_range(2))   # 令x=2，調用方程

　　原諒我糟糕的Python風格，但是我希望代碼清晰，而不是簡潔。

　　**符號表示x的j次冪。方程輸入參數x，我令它為2。從0到5循環，取x的1,2,3,4, 5次冪，然後將這些數字添加到一個列表中。它得出列表數字之和為：62。

　　走進矩陣

　　記住，2D張量也被稱為矩陣。它基本上是一個表格，有行和列。首先，你需要知道如何引用矩陣的不同部分。 這張圖講得很清楚：

　　

　　首先我們有矩陣A。用大寫字母表示。

　　矩陣有m行和n列，所以我們叫它m X n 矩陣，用小寫斜體字母表示。

　　行是水平的，也就是從左到右。 （不要被圖中箭頭迷惑，箭頭指向的i和j不是行的方向，行是水平的！）

　　列是垂直的，也就是從上到下。

　　在這個例子中我們有一個4 x 5 矩陣，（也就是2D張量），因為我們有4行5列。

　　每個方格是矩陣中的一個元素。元素的位置使用小寫斜體a和行序號i和列序號j來表示。

　　所以第1行第2列的4，用a1,2表示。第2行第1列的3，用a2,1表示。

　　我們不會講解所有的矩陣數學運算，我們選擇其中一種來小試牛刀。

　　點乘在神經網路中是一種非常常用的運算，所以一起看看它。

　　點，點，點

　　點乘是我們用一個矩陣乘以另一個矩陣的方法。

　　點乘的符號表示，你應該猜到了，是一個點。

　　a . b

　　這是兩個標量(也就是單獨的數)的點乘。標量也是我們的矩陣里的獨立的元素。

　　我們將同樣大小和形狀的矩陣對應的元素相乘，再把所有的乘積作和。

　　那麼一個向量和另一個向量乘積的公式是什麼樣的呢？

　　

　　深吸一口氣。你成功了！

　　我們現在認識了所有的符號。

　　這是兩個等長向量的乘積公式。記住在數學菜鳥的AI學習攻略第四部分-張量表示（有貓） 中講到，一個向量就是一行或者一列數字。我們的矩陣的每一行或者每一列都是一個向量。

　　首先我們用矩陣A的第一個元素乘以矩陣B的第一個元素。然後我們用元素A2 乘以元素B2.我們對於每一個元素做相同的操作，直到達到末尾，「n」。然後對它們作和。

　　讓我們看一下這個操作的圖示。

　　

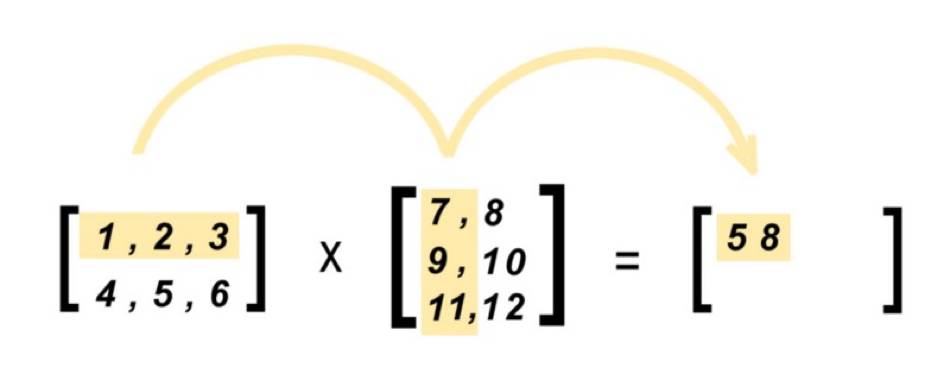
　　現在我們可以把這些數字代入我們的公式。

　　

　　這裡是輸出矩陣下一個數字的例子

　　

　　

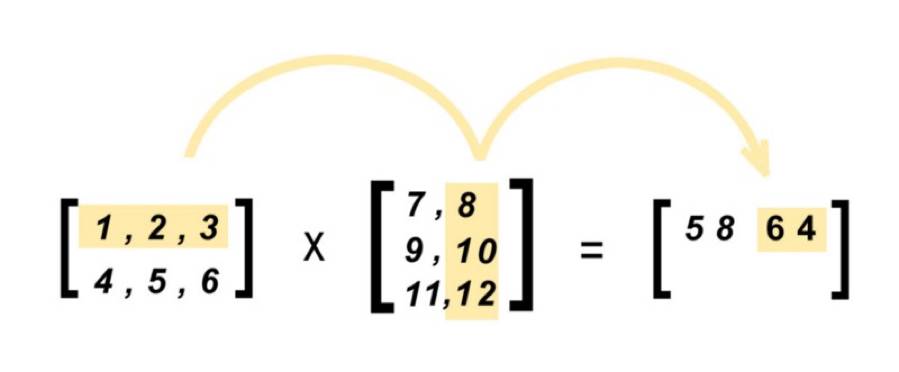
　　這是我們處理完所有運算得到的最終結果：

　　

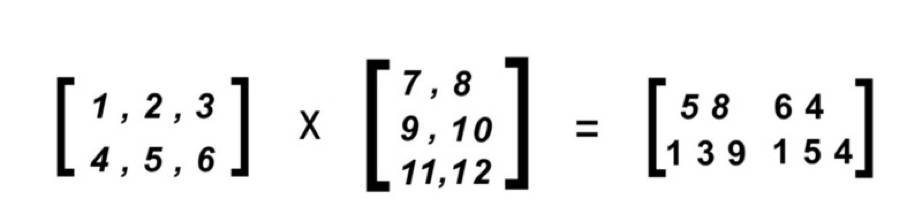
　　這些例子來自於神奇的趣味數學網站（Math is Fun website）。這個網站里有大量超贊的例子，完全無法超越。

　　我增加了一些公式，以助於你的理解。因為他們一般都會跳過這些，因為一般這些步驟並不會令人感到困惑。但是你現在再也不會困惑了。

　　勝在學習策略

　　我想用一些可以幫你快速學習的策略來結束這篇文章。

　　我是一個自學者，也就是我一般自己給自己講解。當我可以放慢腳步，可以自己探索時，我可以學得更好。我會犯一些錯誤。我上一篇文章就是一個很好的例子，我不得不修正一部分。但是錯誤也是一件好事！

　　錯誤是過程中的一部分。你沒有辦法避免錯誤，只能擁抱它。你犯錯了，你會進步。沒有犯錯，就沒有進步。就是這麼簡單。

　　工程界有一個老段子。

　　如果你想知道正確答案，不用請人幫忙。只要將錯誤答案發出來，你就可以看看多少工程師跳出來指正你！

　　工程師絕不允許錯誤答案存在！

　　這是一個老段子，但是常常很管用。

　　另一件重要的事情是，如果你沒有讀我在數學菜鳥的AI攻略的一部分推薦的文章的話，或者你沒有微積分、代數和幾何背景的話，你可能讀不了數學符號書（Mathematical Notation book） 。你需要懂得一個術語的背景知識。但是我建議你買一本，它可以在你讀其他書的時候，作為一個參考指南。

　　另外，建議放慢腳步。這又不是比賽！半途而廢等於沒有分。如果你跳過了一些你不懂的術語，你將來還是不得不回頭來看。

　　所以停下來，花一點時間搞明白所有你不懂的符號。這很緩慢，甚至令人沮喪。但是當你建立越來越多的知識體系，你會越來越快。你會發現你已經理解了一些術語，而此前你從未想象自己可以理解它。

　　另外，你可能需要從多個地方來查詢。需要面對的事實是，大部分人都不是好老師。他們可能理解了一篇材料，但是並不意味著他們可以給其他人講清楚。教學是一門藝術。這就是為什麼趣味數學網站比維基百科好。維基百科確實很「正確」，但是也很枯燥，有時候還令人費解。等你學到更多的時候，也許你可以將維基百科改得更好。

　　將這些忠告記在心裡，你的AI學習之旅就不會誤入歧途！

　　來源：https://hackernoon.com/learning- ... d76a1fe5#.1doldcnhr

　　

　　關於轉載如需轉載，請在開篇顯著位置註明作者和出處（轉自：大數據文摘 | bigdatadigest），並在文章結尾放置大數據文摘醒目二維碼。無原創標識文章請按照轉載要求編輯，可直接轉載，轉載后請將轉載鏈接發送給我們；有原創標識文章，請發送【文章名稱-待授權公眾號名稱及ID】給我們申請白名單授權。未經許可的轉載以及改編者，我們將依法追究其法律責任。聯繫郵箱：zz@bigdatadigest.cn。志願者介紹

　　回復「志願者」了解如何加入我們

　　

　　往期精彩文章

　　點擊圖片閱讀文章

　　小白學數據 | 28張小抄表大放送：Python,R,大數據,機器學習