如何求彎曲時空的曲率？廣相論37

《 場方程和微分幾何·廣相論37》 

  6、場方程和微分幾何 

場方程是建立在微分幾何基礎上的，

微分幾何水平不行，對一些概念是難以理解的。

對微分幾何，愛因斯坦也是在創立場方程過程中，

向他的數學家朋友現學的。

微分幾何是運用微積分來研究空間幾何性質的數學。

古典微分幾何起源於微積分，

內容是『曲線論』和『曲面論』。

歐拉、蒙日和高斯，是古典微分幾何的奠基人；

而近代微分幾何的創始人是黎曼。 

黎曼在1854年創立了黎曼幾何，

黎曼幾何是近代微分幾何的主要內容。

歐拉（Euler，1707－1783），瑞士數學家。

蒙日（Monge，1746～1818），法國數學家、物化學家。

高斯（英語：Gauss 1777－1855）， 德國數學家、天文學家。

黎曼 ( 1826—1866 )，德國數學家 

通過學習，我們了解到，場方程的計算，離不開黎曼幾何

（黎曼幾何就是彎曲空間幾何）。

1916年愛因斯坦創立了『引力場方程』，

引力場方程是一個二階張量方程，

或者說，引力場方程是一個

二階非線性偏微分方程*。

場方程是用『張量微積分』表述的。 

所謂『張量微積分』 

就是用張量場表述的微分方程。 

  【回顧與複習】

假設彎曲空間，有兩個點，靠得很近，

就可以把它寫成微分形式

（例如，可以把『微小距離』寫成 ds 形式。

就是說，數學符號ds表示空間彎曲程度的極小距離）。

在微分幾何中，

求彎曲空間曲線的長度（弧長），

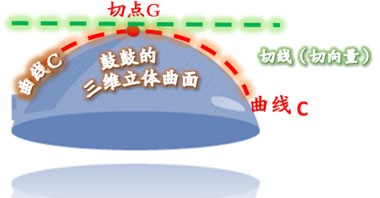
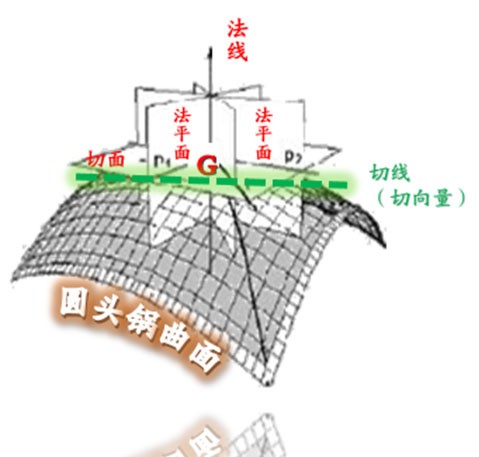
需要先定義某一點的『切向量』長度（參看下面3幅圖）， 

然後，把這條『切向量』所經過的 

所有『微元距離』ds，用微積分算一下，

就可以求出『特定的線段』或『角度』來。

就是說，場方程包含了運用曲線坐標的微分計算

從而得出彎曲時空的曲率。

曲線在某點的『切向量』可以理解為

沿曲線在該點的『切線方向』的『向量』。

『切向量』是與曲線相切的『向量』。 

可以通俗理解為

切向量是與法線相互垂直的線， 

即曲線的法線是垂直於切線的。 

    謝謝閱讀。

• [12/21]缺憾才是美；華嚴頌：不為自己求安樂、但願眾生得離苦
• [12/24]高維空間與生命、聖誕快樂！
• [12/29]當你是地球之心時 人變年輕了！
• [12/31]2020歡樂大跨年；微積分簡介 廣義相對論36
• [01/03]河洛淺談：河圖與洛書是外星文明遺留下來的嗎？
• [01/03] 如何求彎曲時空的曲率？廣相論37
• [01/05]川普：為止戰、非宣戰；河圖與洛書是外星文明遺留下來的嗎？（2）
• [01/08]美國國防部長埃斯珀：不求戰、戰必勝！
• [01/08]美國做好回擊伊朗報復的準備
• [01/10]特斬蘇萊曼尼；死生者，無象在天，以性為主
• [01/13]埃及生命女神；人體經絡與天球經絡相對應
• [01/19]瞬間變化率：什麼是微分方程和偏微分方程？
• [01/24]為武漢祈禱 為世界祈禱 今日只有祈禱

• 查看：[和顏清心的.最新博文]
• 查看：[大家的.最新博文]
• 查看：[大家的.信仰見證]